变换矩阵（Transformation matrix）详解

当我们对一个图形进行平移再旋转，一般流程是需要重新求取一个新的等式，然后实现一个新的着色器，这样很不好。
好在我们可以使用另一个数学工具—变换矩阵（Transformation matrix）来完成这项工作。变换矩阵非常适合操作计算机图形。
一、旋转矩阵
当p按照右手法则逆时针旋转β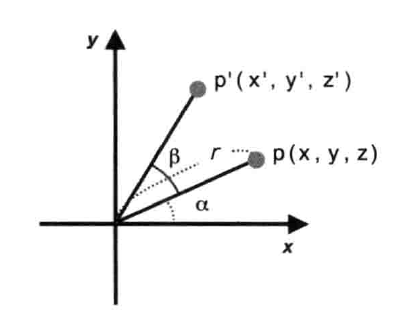

p点的坐标计算为：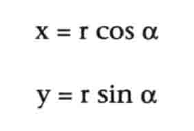

p`点坐标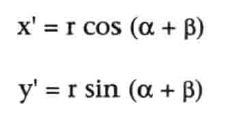

分解后，即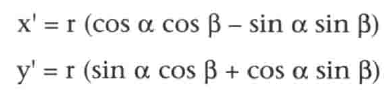

基于第一个公式，消掉r和α，得：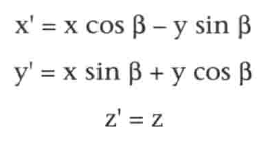

通过以下矩阵相乘可以表示该过程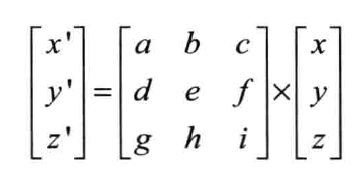

综合以上两个公式：
我们可以令
a=cosβ，b=-sinβ,c=0,d=sinβ,e=cosβ,f=0,g=0,h=0,i=1,
可得：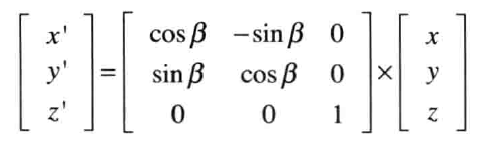

二、平移矩阵
一般平移矩阵计算为：

相乘得到：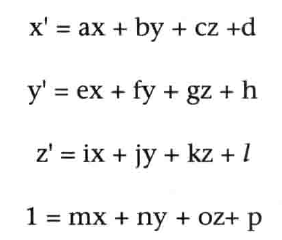

比较以下等式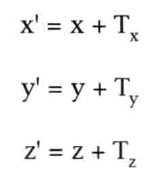

我们可以令：
a=1,b=0,c=0,d=Tx,
e=0,f=1,g=0,h=Ty,
i=0,j=0,k=1,l=Tz,
m=0,n=0,o=0,p=1,
可得：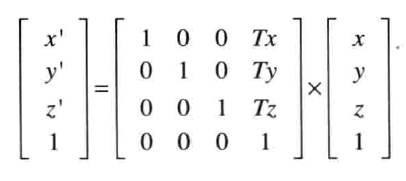

三、缩放
假设X轴、Y轴、Z轴缩放因子Sx,Sy,Sz,那么有：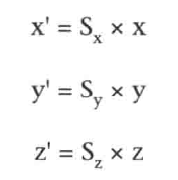

即有缩放变换矩阵：

四、旋转+平移+缩放
至此，我们已经推演出一个旋转矩阵和一个平移矩阵、一个缩放矩阵，但是我们发现旋转矩阵是3x3，平移缩放矩阵是4x4, 于是需要将旋转矩阵转变为4x4矩阵，我们知道最后一个分量w的加和结果应为1
所以：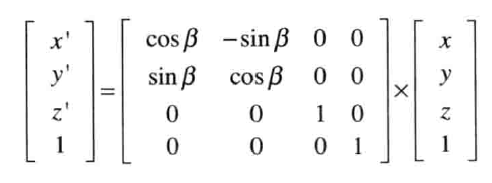

所以在程序中定义一个旋转+平移+缩放矩阵，可以按照以下写：
注意WebGL中矩阵是列主序的，即为上面矩阵的转置

const canvas=document.getElementById('webgl');
const gl=getWebGLContext(canvas);
let VSHADER_SOURCE=
    'attribute vec4 a_postion;\n' +
    'uniform mat4 u_panMatrix;\n' +
    'uniform mat4 u_rotateMatrix;\n' +
    'uniform mat4 u_zoomMatrix;\n' +
    'void main () {\n' +
    ' gl_Position = u_panMatrix * u_rotateMatrix * u_zoomMatrix * a_position;\n' +
    '}\n';

const radian=Math.PI*ANGLE/180.0 // 角度值转弧度
const cosβ=Math.cos(radian);
const sinβ=Math.sin(radian);
const Sx = 1.0, Sy = 1.5, Sz = 1.0;

// 平移矩阵
const pan=new Float32Array([
    1.0, 0.0, 0.0, 0.0,
    0.0, 1.0, 0.0, 0.0,
    0.0, 0.0, 1.0, 0.0,
    Tx, Ty, Tz,1.0
]);

// 旋转矩阵
const rotate=new Float32Array([
    cosβ, sinβ, 0.0, 0.0,
    -sinβ, cosβ, 0.0, 0.0,
    0.0, 0.0, 1.0, 0.0,
    0.0, 0.0, 0.0, 1.0
]);

// 缩放矩阵
const zoom=new Float32Array([
    Sx, 0.0, 0.0, 0.0,
    0.0, Sy, 0.0, 0.0,
    0.0, 0.0, Sz, 0.0,
    0.0, 0.0, 0.0, 1.0
])

const u_panformMatrix=gl.getUniformLocation(gl.program, 'u_panMatrix');
const u_rotateMatrix=gl.getUniformLocation(gl.program, 'u_rotateMatrix');
const u_zoomMatrix=gl.getUniformLocation(gl.program, 'u_panMatrix');
gl.uniformMatrix4fv(u_panformMatrix, false, pan);
gl.uniformMatrix4fv(u_rotateMatrix, false, rotate);
gl.uniformMatrix4fv(u_zoomMatrix, false, zoom);