关于多圆（大于2）重叠的面积计算

这个问题是我在计算公交站点覆盖率（公交300米范围面积/服务区面积）中遇到的。
有以下两种计算方式

1、ArcGIS
使用buffer（缓冲区）工具，将所有的公交站点生成300米的缓冲圆
缓冲区
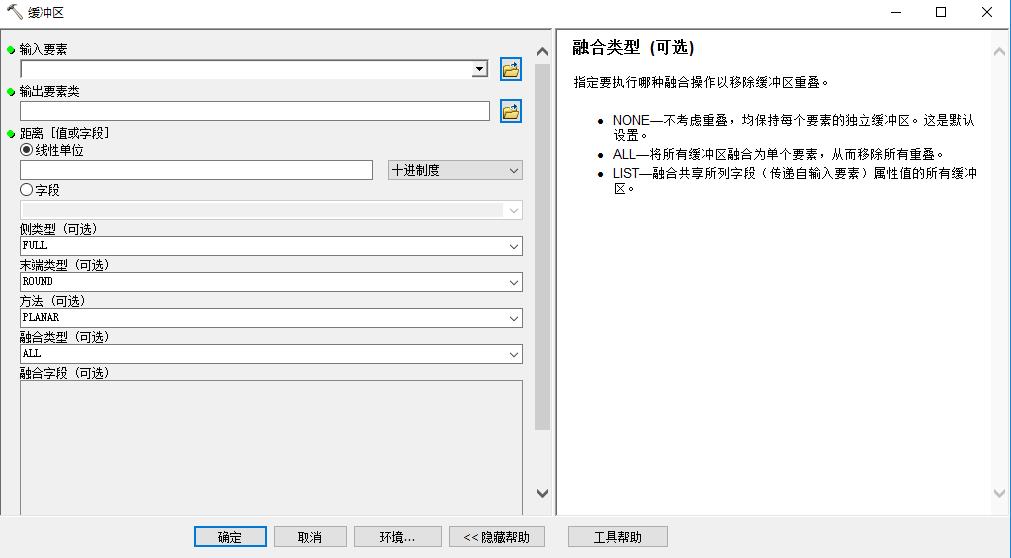
注意：融合类型选择为全部

2、自己实现
之前以为这个计算应该不难，用纯数学计算就可以求得结果，但是接下来的问题让我陷入了对人生的思考，经过查找文献，得到以下结论。
1）两圆重叠—简单！！！
2）两个圆以上的重叠精确计算—数学界的世纪难题！！！
多圆重叠面积
所以，只能通过模拟计算，这也是计算机最初诞生的原因。
经典的蒙特卡洛模拟计算真是屡试不爽。

这里我以前端的JavaScript为例
情景：在地图上随机框画了一个圆形区域，框选区域内部有若干个公交站点
通过模拟计算的流程是这样：
画圆

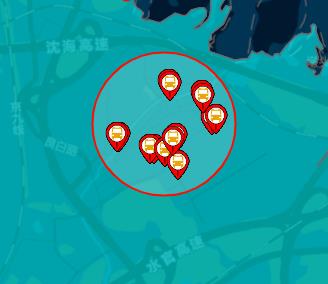
代码脚本如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * 使用蒙特卡洛方法模拟计算站点覆盖率
 * @param sample 样本数
 * @param drawCircleToPolygon 所画区域外接多边形
 * @param stopsLngLatList 所画区域内站点坐标
 * @param distance 站点覆盖半径
 * @returns {string} 返回站点覆盖率
 */
function calculateStopCoverRate(sample, drawCircleToPolygon, stopsLngLatList, distance) {
  let insidePointsNumber = 0;
  let randomPoints = turf.random('points', sample, {bbox: drawCircleToPolygon.getExtent()}).features.map(value => value.geometry.coordinates);
  for (let m = 0, n = randomPoints.length; m < n; m++) {
    for (let i = 0, j = stopsLngLatList.length; i < j; i++) {
      let centerRandomPoint = ol.proj.fromLonLat([randomPoints[m][0], randomPoints[m][1]]);
      if (Math.pow(centerRandomPoint[0] - stopsLngLatList[i][0], 2) + Math.pow(centerRandomPoint[1] - stopsLngLatList[i][1], 2) <= distance * distance) {
        insidePointsNumber = insidePointsNumber + 1;
        break
      }
    }
  }
  return (insidePointsNumber / sample * 100).toFixed(2) + ' %';
}

1）首先引入turf插件，使用turf.random在所画的圆内生成随机点，获取每个随机点的坐标；
2）使用openlayers的ol.proj.fromLonLat转换方法，将经纬度转为平面坐标；
3）计算随机点是否在圈出的站点300米（distance）范围内，如果在，标记一下，break该点退出，计算下一个随机点，
4）用标记到在站点范围的统计数值insidePointsNumber除以样本值就是站点覆盖率，
5）同样,覆盖面积就等于所画圆的面积乘以覆盖率

**
sample 样本数数值越大，所需时间越长，计算结果越准确

关于蒙特卡洛，有很多有趣的事，比如计算Π值，古代的蒲丰投针
计算Π

相比精确的数学计算，模拟计算有点玄学的意味，但不失为简单粗暴的途径。